Often in engineering and computer science, one wants to optimize a system. For instance, what is the perfect combination of ingredients to create the best tasting drink? How could we both increase the speed and reduce the energy consumption of a server or design the perfect car?

These problems, or systems, are complex, and often have more than 2 input variables. How should one change each of these variables? An idea that springs to mind, is increase the first input variable by a small number, and see if that improves things. However, should you increase or decrease the second input? In a system with two inputs (say sugar and water in a drink) this isn’t so complicated.

You could try many different combinations and hope to find an optimum. This technique is known as brute force search. In some cases, this can work well. However, in cases with a high number of variables, this can prove impossible to compute on standard computing (sometimes taking millennia to compute).

However, with a bit of help from nature, we can use an evolutionary approach to choose the best inputs. Just as, over time, wings on birds became more streamlined, and better at flying, we can simulate the same on computers.

This approach trials a population (say 100 different combinations of inputs), selects the best few (say 10), mates these ten and induces mutations at a random interval. Now we have a totally new population with similar characteristics of the best parents. This is how evolution works, and can be applied in computer science for optimizing input variables to get the best output.

In the case of a single output objective, it is easy to do, you just select the 10 best individuals based on their output score from a function or equation. However, when you have multiple objectives, one solution may be optimum for one person’s taste, but not for another. How can we select solutions that are optimum for every single person’s taste?

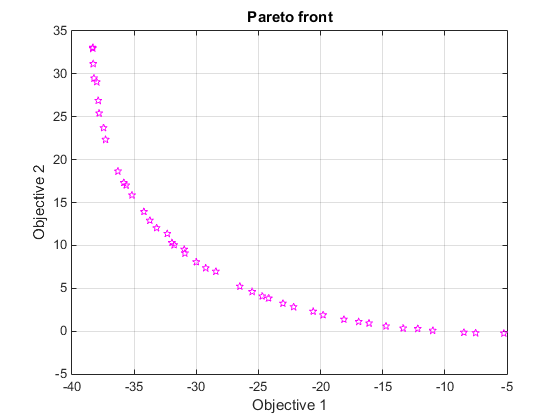
This is where the Pareto Front comes in. As can be seen in the image below, a Pareto Front, finds a wide number of objectives suited for every persons need. Let’s say, for example, that objective one is sweetness, and objective two is tasteless. You could change the amount of water and sugar an infinite number of ways, but which are the best?

This is where the Pareto Front comes in. We select the best individuals over time to suit everybody’s needs.

To actually achieve this Pareto Front with a genetic algorithm can get a bit technical and out of the scope of this paper. But I encourage you to look at the paper on the NSGA-II algorithm, linked here if you are interested to learn more.

There are many different types of ways these algorithms that can be applied to optimise systems, and I have left a link of a paper I did during my PhD to optimise the speed and energy use of multiple computers.